Rumus Sudut Ganda atau Rangkap part1 Lengkap_Trigonometri

Untuk 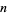bilangan bulat positif, ekspresi dari bentuk 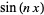. 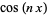, Dan 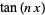dapat dinyatakan dalam hal 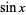dan 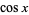hanya menggunakan rumus Euler dan teorema binomial . Untuk .

			(1)
			(2)
			(3)
			(4)
			(5)
			(6)

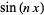Beberapa nilai pertama diberikan oleh

			(7)
			(8)
			(9)
			(10)

Formula terkait lainnya termasuk

			(11)
			(12)

di mana 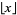adalah fungsi Floor .
Sebuah formula produk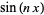 diberikan oleh

(13)

Fungsi 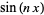juga dapat dinyatakan sebagai polinomial dalam 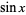(Untuk 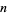aneh) atau 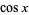kali polinomial di 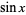sebagai

(14)

di mana 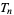adalah polinomial Chebyshev jenis pertama dan 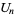adalah polinomial Chebyshev jenis kedua . Beberapa kasus pertama adalah

			(15)
			(16)
			(17)
			(18)

Demikian pula, 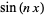dapat dinyatakan sebagai 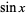kali polinomial di 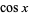sebagai

(19)

Beberapa kasus pertama adalah

			(20)
			(21)
			(22)
			(23)

Bromwich (1991) memberikan rumus

(24)

di mana .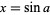
Untuk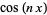 , Rumus multiple-angle dapat diturunkan sebagai

			(25)
			(26)
			(27)
			(28)
			(29)
			(30)

Beberapa nilai-nilai yang pertama adalah

			(31)
			(32)
			(33)
			(34)

Formula terkait lainnya termasuk

			(35)
			(36)
			(37)

Fungsi 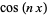juga dapat dinyatakan sebagai polinomial dalam 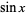(Untuk 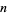bahkan) atau 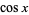kali polinomial di 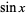sebagai

(38)

Beberapa kasus pertama adalah

			(39)
			(40)
			(41)
			(42)

Demikian pula, 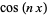dapat dinyatakan sebagai polinomial dalam 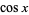sebagai

(43)

Beberapa kasus pertama adalah

			(44)
			(45)
			(46)
			(47)

Bromwich (1991) memberikan rumus

(48)

di mana .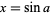
Beberapa formula multi-angle pertama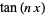 adalah

			(49)
			(50)
			(51)

diberikan oleh Beyer (1987, hal. 139) sampai .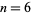
Formula Multiple-sudut juga dapat ditulis dengan menggunakan hubungan recurrence 

			(52)
			(53)

Mencari rumus sudut ganda sin (nα), cos (nα), tan (nα) 

1)             Sin 2α = sin(α+α) = sin α.cos α + cos α. sin α = 2.sin α.cos α
sin 2α = 2sin α.cos α (terbukti)

2)             Cos 2α = cos(α+α) = cos²α - sin²α = cos²α -(1- cos²α) = cos²α -1+cos²α

        cos 2α = 2cos²α - 1 (terbukti)

3)             Cos 2α = cos²α - sin²α = (1 - sin²α) - sin²α = 1- sin²α - sin²α
cos 2α = 1-2sin²α (Terbukti)

4)             Cos 2α = cos(α+α) = cosα.cosα – sinα.sinα = 
cos 2α = cos²α - sin²α (terbukti)

5)             Tan 2α = (tan α+ tan α)/(1- tan α. tan α)
Tan 2α= (2 tan α)/(1-tan²α) (terbukti)

6)             Tan 2α = sin 2α/cos 2α = (2sinα.cosα)/(cos²α - sin²α) = {2[(sinα.cosα)/cos²α]}/{(cos²α/cos²α) - (sin²α/cos²α)} =
Tan 2α= (2 tan α)/(1-tan²α) (terbukti)

7)             Tan 2α = {2tanα}/(1-tan²α} = {2tanα(1/tanα)}/{(1-tan²α)(1/tanα)} = 2/{(1/tanα) – (tan²α/tanα)} = 2/{cotα – tanα}

        Tan 2α = 2/{cotα – tanα} (terbukti)

8)             Tan 2α = 2/{cotα – tanα} = (2 tan α)/(1-tan²α) = {2cotα}/{cot²α – 1}

9)             Cosec 2α = 1/(sin 2α) = 1/(2sin α.cos α) = 1/2 csc α. sec α
Cosec 2α = 1/2 cosec α. sec α (Terbukti)

10)         cosec 2α = cosec (α+α) = (cosecα.cosecα)/(cotan α+cotan α) = (cosec²α)/(2cot α)
cosec 2α = (cosec²α)/(2cot α) atau (cot²α + 1)/(2cot α) (terbukti)

11)         Cosec 2α = 1/{2sinαcosα} = {cosec²α}/{2cotα} = sec²α/2tanα = {1+cot²α}/{2cotα} = {1+tan²α}/{2tanα}

12)         Cosec 2α = 1/sin2α = 1/(2sinαcosα) = (cosα)/(2sinαcos²α) = {sec²α}/{2(sinα/cosα)} = (sec²α)/(2tanα) = (1+tan²α)/(2tanα)

Cosec 2α = (1+tan²α)/(2tanα)

13)         Cosec 2α = 1/sin2α = (sin²α + cos²α)/(2sinα.cos α) = 1/2 tan α + cot α

14)         Sec 2α = 1/(cos 2α) = 1/(cos²α - sin²α) = 1/((1/sec²α)-(1/cosec²α))

          = 1/((cosec²α-sec²α)/(sec²α.cosec²α)) = (sec²α . cosec²α)/(cosec²α-sec²α)
Sec 2α = (sec²α . cosec²α)/(cosec²α-sec²α) (Terbukti)

15)         sec 2α = sec(α+α) = (secα.secα)/(1-tanα.tanα) = (sec²α) / (1-tan²α)
sec2α = (sec²α)/(1-tan²α) atau (1+tan²α) / (1-tan²α)(terbukti)

16)         sec 2α = 1/{cos²α-sin²α} = 1/{2cos²α-1} = 1/{1-2sin²α}

17)         sec 2α = {sec²α}/{1-tan²α} = {cosec²α}/{cot²α-1} = {1+tan²α}/{1-tan²α} = {1+cot²α}/{cot²α-1}

18)         sec 2α = 1/cos 2α = 1/(cos²α-sin²α) = (cos²α+sin²α)/(cos²α - sin²α) = {(cos²α/cos²α)+(sin²α/cos²α)}/{(cos²α/cos²α)-(sin²α/cos²α)} = {1+tan²α}/{1-tan²α}

sec 2α = {1+tan²α}/{1-tan²α} terbukti

19)         cotan 2α = 1/ tan 2α = 1/ tan (α+α) = 1/ (2tan α/(1-tan²α)) = 1-tan²α / 2 tanα
            cotan 2α = 1-tan²α / 2 tanα

          * lanjutan cotan 2α, = (1-(1/cot²α))/ (2.(1/cot α))
= (cot α.cotα -1)/ (cotα + cotα) = (cot²α -1 /cot²α) x (cot α/2)

cotan 2α  =  (cot²α -1)/(2 cot α) atau (1-tan²α)/(2tan α) atau (cot α-tanα)/2 (Terbukti)

20)         cotan 2α = cot(α+α) = (cot α.cot α -1) / (cotα+cotα)

          cotan 2α = (cot²α -1) / (2 cot α) (terbukti)

21)         cotan 2α = cos 2α/sin 2α = {cos²α - sin²α}/{2sinαcosα} = (cosαcosα/2sinαcosα) – (sinαsinα/2sinαcosα) = (cosα/2sinα) – (sinα/2cosα) = ½ (cotα – tanα)

22)         cotan 2α = cos 2α/sin 2α = (cos²α - sin²α)/ 2 (sinαcosα) = ½ {(cosα/sinα) – (sinα/cosα)}

cotan 2α = ½ (cotα – tanα)

23)         cotan 2α = {cotα – tanα}/2 = {1-tan²α}/{2tanα} = {cot²α-1}/{2cotα}

24)         Sin 3α = sin (α + 2α)
            = sin α cos 2α + sin 2α cos α
            = sin α (1 - 2 sin² α) + (2 sin α cos α) cos α
            = sin α - 2 sin³ α + 2 sin α cos² α
            = sin α - 2 sin³ α + 2 sin α (1 - sin² α)
Sin 3α = 3 sin α - 4 sin³ α (terbukti)

25)         Sin 3α = sin ( 2α + α)= sin 2α.cos α + cos2α.sin α

= (2sin α.cos α)cos α + (1-2.sin²α).sin α

= 2.sin α.cos² α + sin α - 2. sin³ α

          = 2.sin α(1 – sin²α) + sin α –2.sin³α
= 2.sin α –2.sin ³α + sin α –2.sin ³α

      Sin 3α = 3.sin α –4.sin³α (terbukti)

26)         Sin 3 α= sin (2α+α)
             = sin 2α cos α + cos 2α sin α
             = 2 sin α cos α cos α + (1-2 sin² α) sin α
             = 2 sin α cos²α + sin α - 2sin³ α
             = 2 sin α(1 - sin²α) + sin α - 2sin³ α
            = 2 sin α - 2sin³ α + sin α - 2sin³ α
Sin 3α = 3 sin α - 4 sin³ α (terbukti)

27)         Sin (3α) = sin(α+2α) = sin(α).cos(2α) + cos(α).sin(2α)
= sin(α)(cos²(α) − sin²(α)) + cos(α)(2sin(α)cos(α))

= sin(α)cos²(α) − sin³(α) + 2sin(α)cos²(α)

sin 3α = 3sin(α)cos²(α) − sin³(α) (Terbukti) 

28)         Sin 3α = 3cos²α.sinα – sin³α = 3(1-sin²α)sinα – sin³α = 3sinα – 4sin³α

29)         Sin 3α = sin(α+2α) = sinα.cos2α + cosα.sin2α = sinα(cos²α − sin²α) + cosα(2sinα.cosα)

= cos²α.sinα − sin³α + 2cos²α.sinα = 3cos²α.sinα - sin³α = sinα(3cos²α-sin²α) = sinα(3(1-sin²α)-sin²α) = sinα(3-4sin²α) = 3sinα – 4sin³α

Sin 3α = 3sinα – 4sin³α

30)         Cos 3α = cos³α – 3cosα.sin³α = cos³α – 3cosα(1-cos²α) = 4cos³α – 3cosα

31)         Cos 3α = cos (2α+α)
              = Cos2α.cosα - sin2α.Sinα
              = (2cos²α-1)Cosα - 2sin²α.cosα
              = 2cos³α - Cosα - 2(1-cos²α)Cosα
              = 2cos³α - Cosα - 2cosα + 2cos³α
Cos 3α  = 4cos³A - 3cosA (Terbukti)

32)         Cos 3α = cos(α+2α) = cos(α)cos(2α) − sin(α)sin(2α)
= cos(α)(cos²(α) − sin²(α)) − sin(α) x 2 sin(α)cos(α)
= cos³(α) − sin²(α)cos(α) − 2 sin²(α)cos(α)

          cos 3α = cos³(α) − 3 sin²(α)cos(α) (terbukti)

33)         Cos 3α = cos(α+2α) = cosα.cos2α – sinα.sin2α = cosα(cos²α − sin²α) – sinα(2sinα.cosα)
= cos³α − cosα.sin²α − 2cosα.sin²α = cos³α − 3cosα.sin²α = cosα(cos²α – 3sin²α) = cosα(cos²α – 3(1-cos²α)) = cosα(cos²α – 3+3cos²α) = cos α (4cos²α-3) = 4cos³α – 3cosα

Cos 3α = 4cos³α – 3cosα

34)         Tan (3α) = Tan (2α + α)
               = (2tan α / (1-tan²α) + Tan α) / (1 - 2tan²α / (1-tan²α))
              = (2tanα + Tan α (1-tan²α)) / ((1-tan²α) - 2tan²α)
             = (2tanα + Tan α - tan³α) / (1 - 3tan²α) 
Tan 3α = (3tan α - tan³α) / (1 - 3tan²α) (terbukti)

35)         Tan 3α = sin 3α / cos 3α
          = Sin (2α+α)/cos (2α+α)
           = [Sin 2αcos α + cos2α.sin α] / [cos2αcosα - sin2αsinα]
           = [2sin α.cos²α + cos ²α.sin α - sin³α] / [cos³α - sin²α.cos α - 2sin²α.cos α]
            = [3sin α.cos ²α - sin ³α] / [cos³α - 3sin²α. cos α]
Membagi pembilang dan penyebut dengan cos ³α untuk mendapatkan:
            = [3sin α. cos²α/cos³α - sin³α/cos³α]/[cos³α/cos³α - 3sin²α.cosα/cos³α]
           = [3sin α / Cos α - tan ³α] / [1 - 3sin²α/cos²α]  
Tan 3α = [3tan α - tan ³α] / [1 - 3tan ²α] (terbukti)

36)         Tan 3α = tan(2α+α) = (tan2α+tanα)/(1- tan2α.tanα) 
            = {[(2tanα)/(1-tan² α)]+ tan α}/{1-(2tan α/1-tan² α)(tan α)}
  = {[(2tan α)/(1-tan² α)]+{[(1-tan² α)tan α]/(1-tan² α)}/{[(1-tan² α)/ (1-tan² α)]-[2tan² α/(1-tan² α)]} 
            = {[(2tanα + tanα - tan³α)/(1-tan²α)]/[(1-tan²α - 2tan²α)/(1 - tan²α)]} 
            = {2tanα + tanα - tan³α}/{1 - tan²α - 2tan²α} 
Tan 3α = {3tan α – tan³α}/{1-3tan²α} (Terbukti)

37)         Tan 3α = sin 3α/cos 3α = {3cos²α.sinα – sin³α}/{cos³α – 3cosαsin³α} = {sinα(3cos²α -sin²α)}/{cosα(cos²α -3sin²α)} = {sinα(3-tan²α)}/{cosα(1-3tan²α)} = {(sinα/cosα)(3-tan²α)}/{1-3tan²α} = {tanα(3-tan²α)}/(1-3tan²α)

Tan 3α = {3tanα – tan³α}/{1-3tan²α}

38)         Tan 3α = tan(2α+α) = (tan2α + tanα)/(1- tan2α.tanα) = {([2tanα/1-tan²α]+ tan α)(1-tan²α}/[{1-(2tan α/1-tan²α)(tanα)}(1-tan²α)] = = {2tanα + tanα - tan³α}/{1 - tan²α - 2tan²α} = {3tanα – tan³α}/{1-3tan²α}

39)         cosec 3α = 1/(sin 3α) = 1/(3sin α - 4sin³α) atau (cosec³α)/(3cot²α - 1)

40)         sec 3α = 1 /cos (3α) = 1 /(4cos³α - 3cosα) atau (sec³α)/(1 - 3tan²α)

41)         Cot 3α = cos 3α/sin 3α = {cos³α – 3cosαsin³α}/{3cos²α.sinα – sin³α} = {cot³α – 3cot α}/{3cot²α – 1}

42)         Cotan 3α, ingat Tan 3α = {tanα + tan 2α}/{1 – tanα .tan 2α} = {(tan α+ 2tanα)/(1 – tan²α)}/{(1 – tanα.2tanα)/(1 – tan²α)} = {tan α(1 – tan²α)+2tanα}/{1 – tan²α – 2tan²α} = {3tan α – tan³α}/{1 – 3tan²α} = {3 cot²α – 1}/{cot³α – 3cot α}

          Sehingga

          Cot 3α = 1/tan3α = {cot³α – 3cot α}/{3 cot²α – 1} Terbukti

43)         Cotan 3α = cos(3 α)/sin(3 α)

          = [4cos³(α) - 3cos(α)]/[3sin(α) - 4sin³(α)]
Membagi kedua pembilang dan penyebut dengan sin³(α)
= {4(cos³(α)/sin³(α)) - 3(cos(α)/sin³(α))}/{3(sin(α)/sin³(α))-4(sin³(α)/sin³(α))}
=  {4cot³(α) - 3(cos(α)/sin(α))(1/sin²(α))}/{3(1/sin²(α)) - 4}
= [4cot³(α) - 3cot(α)csc²(α)]/[3csc²(α) - 4]
Ingat: csc²(α) - cot²(α) = 1, cot(α) = cos(α)/sin(α),
= [4cot³(α) - 3cot(α){1 + (cot²(α))}]/[3{1 + (cot²(α))} - 4]

          cotan 3α = [cot³(α) - 3cot(α)]/[3cot²(α) - 1]

        cotan 3α = (3cotα - cot³α)/ (1 - 3cot²α) atau (1 - 3tan²α)/ (3tan α - tan³α) (terbukti)

44)         Cot (α+β+ς) = {Re (i+cot α)(i+cot β)(i+cot c)}/{Im (i+cot α)(i+cot β)(i+cot c)}

          = {cotα.cotβ.cotς – cotα – cotβ – cotς} / {cotα.cotβ + cotα.cotς + cotβ.cot ς – 1}

          Cot 3α = {cot³α – 3cot α}/ {3cot²α – 1} Terbukti

45)         Cot 3α = cot (2α+α)

          Dalam tan α = 1/(tan (2α+α) = {1/(tan2α+tan α)}/{1-tan2α.tanα} = (1-tan2α.tanα)/(tan 2α+tan α)

          Dalam cot α = {1-(1/cot 2α)(1/cot α)}/{(1/cot 2α) + (1/cot α)} = {(cot 2α.cot α – 1)/(cot 2α.cot α)}/{(cot α+cot 2α)/(cot 2α.cot α)} = (cot 2α.cot α – 1)/(cot 2α + cot α)

          Cot 3ɑ = (cot 2α.cot α – 1)/(cot 2α + cot α)

46)         Cot 3α = cos 3α/sin 3α = {4cos³α – 3cosα}/{3sinα – 4sin³α} = {[4cos³α – 3cosα]/cos³α}x{1/[3(sinα/cos³α)-4(sin³α/cos³α)]}= {4-(3/cos²α)}/{1/[3(sinα/cosα)(1/cos²α)-4tan³α]} = {4-3(1+tan²α)}/{3tan α(1+tan²α)-4tan³α} = {4-3-tan²α}/{3tanα+3tan³α – 4tan³α} = {1-(1/cot²α)}/{(3/cotα) – (1/cot³α)} = (cot²α-1/cot²α)x(cot³α/3cot²α-1)

Cot 3α = (cot³α – 3cotα)/(3cot²α-1)

47)         Sin 4α = sin 2(2α) = 2sin2α.cos2α = 2(2sinα.cosα)(cos²α - sin²α)
sin 4α = 4sinα.cos³α - 4sin³α.cosα (terbukti)

48)         sin 4a = sin 2(2α) = 2sin2α.cosα = 2(2sinα.cosα)(1-2sin²α)
sin 4α = 4 sin α cos α - 8 sin³ α cos α (terbukti)

49)         Sin 4α = 4cos³αsinα – 4 cosαsin³α = 4cosα(1-sin²α)sinα – 4cosαsin³α = 4cosα(sinα – 2sin³α)

50)         Sin 4α = sin 2(2α) = 2sin2α.cos2α = 2(2sinα.cosα)(cos²α - sin²α) = 4cosα.sinα(cos²α - sin²α) = 4cos³α.sinα – 4cosα.sin³α = 4sinα.cosα(cos²α-sin²α) = 4sinα.cosα{(1-sin²α)-sin²α} = 4sinα.cosα(1-2sin²α) = 4sinα.cosα – 8sin³α.cosα

Sin 4α = 4sinα.cosα – 8sin³α.cosα

51)         Cos 4α = cos⁴α – 6cos²αsin²α + sin⁴α = cos⁴α – 6cos²α(1 – cos²α)+(1 – cos²α)² =

          Cos 4α = 8cos⁴α – 8cos²α + 1

52)         Cos 4α = cos 2(2α) = 2cos²2α – 1 = 2(2cos²α - 1)² - 1 = 2(4cos⁴α - 2cos²α + 1) - 1
             = 8 cos⁴α - 8 cos² α + 2 - 1
cos 4α =  8 cos⁴α – 8 cos² α + 1 (Terbukti)

53)         cos 4α = 1-2sin²2α = 1-2(2sinαcosα)² = 1-8sin²αcosα = 1-8sin²α(1-sin²α)

          cos 4α = 1-8sin²α + 8sin⁴α (terbukti)

54)         cos 4α = cos (2α+2α) = cos2α.cos2α – sin2α.sin2α = cos²2α – sin²2α

                   = (2cos²α – 1)² - (2sinαcosα)² = 4cos⁴α – 4cos²α +1 – 4sin²αcos²α

                   = 4cos⁴α – 4cos²α +1 – 4(1 – cos²α)cos²α = 4cos⁴α – 4cos²α +1 – 4(cos²α - cos⁴α) = 4cos⁴α – 4cos²α +1 – 4cos²α +4cos⁴α

          Cos 4α = 8cos⁴α – 8cos²α +1 (terbukti)

55)         cos 4α = cos (2α+2α) = cos 2α cos 2α – sin2α sin2α = cos²2α – sin²2α = (cos²α - sin²α)² - (2sinα.cosα)² = cos⁴α - 2cos²α.sin²α + sin⁴α - 4cos²α.sin²α = cos⁴α – 6cos²α.sin²α + sin⁴α = cos⁴α - 6cos²α.sin²α + (sin²α)² = cos⁴α – 6cos²α(1-cos²α) + (1-cos²α)² = cos⁴α – 6cos²α + 6cos⁴α + 1 – 2cos²α + cos⁴α = 8cos⁴α – 8cos²α + 1

cos 4α = 8cos⁴α – 8cos²α + 1

56)         cos 4α = cos 2(2α) = cos²2α - sin²2α = (cos²α - sin²α)² - (2sinα.cosα)²
= cos⁴α - 2sin²α.cos²α + sin⁴α - 4sin²α.cos²α

          cos 4α = cos⁴α + sin⁴α - 6sin²α.cos²α

57)               57) Kita tahu tan 2α = 2tan α / (1-tan²α)
 Dengan ini kita dapat menulis,
 Tan 4α = tan2 (2α)
      = 2 tan2A / (1- tan² 2α) ............ (1)
     tan2α = 2tan α / (1- tan² α) ............... (2)
Padukan (2) dalam (1)
2 [2tan α / (1- tan² α)]
= -------------------------------------...
1- [2 Tan α / (1- tan²α)]²
4 Tan α / (1- tan²α)
= ----------------------------------------...
[(1- tan²α)² - 4tan²α]/(1-tan²α)²

[Salib multiply di penyebut, sekarang salah satu 1- tan²α akan dibatalkan]
4tan α
= ----------------------------------------...
[1 + tan⁴α - 2tan²α 4tan²α] / (1-tan²α)
Penyebut dari penyebut adalah pembilang
= 4tan α (1- tan²α) / [1 - 6tan²α + tan⁴α]
Tan 4α = (4 Tan α - 4 tan³α) / [1- 6tan²α + tan⁴α] (terbukti)

58)         Tan 4α = sin 4α/cos 4α = {4cos³αsinα – 4 cosαsin³α}/{cos⁴α – 6cos²αsin²α + sin⁴α} = {4(cos³αsinα/cos⁴α)-4(cosαsin³α/cos⁴α)}/{(cos⁴α/cos⁴α) – 6(cos²αsin²α/cos⁴α)+(sin⁴α/cos⁴α)} =

          Tan 4ɑ = {4tanα – 4 tan³α}/{1-6tan²α + tan⁴α} = {4tanα(1-tan²α)}/{1-6tan²α + tan⁴α}

59)         Tan4α = ingat tan 2α = {2tanα}/{1-tan²α} maka,

          Tan4α = tan 2(2α) = {2tan2α}/{1-tan²2α} = {2(2tan α/1-tan²α)}/[1-{2tan α/(1-tan²α)}²] = (4tan α/(1-tan²α)) / [1-{4tan²α/(1-tan²α)²}] = {4tan α/(1-tan²α)} / [{(1-tan²α)² - 4tan²α}/(1-tan²α)²] = {4tan α (1-tan²α)}/{(1-tan²α)² - 4 tan²α} = {4tan α (1-tan²α)}/{1+tan⁴α – 2tan²α – 4tan²α}

          Tan 4ɑ = {4tan α – 4tan³α}/{1 – 6tan²α +tan⁴α}

60)         Cot 4α = ingat teorema de moivre dimana n integer

          (cos α+isinα)ⁿ = cos (nα) + isin(nα) →n = 4

          Maka (cos α+isinα)⁴ = cos 4α + isin 4α = cos⁴α + 4icos³αsinα - 6cos²αsin²α – 4i cosαsin³α + sin⁴α = {cos⁴α – 6cos²αsin²α + sin⁴α} + i{4cos³αsinα – 4 cosαsin³- }

          Cotan 4α = cos 4α/sin 4α = {cos⁴α – 6cos²αsin²α + sin⁴α}/{4cos³αsinα – 4 cosαsin³α} = {(cos⁴α/sin⁴α) – (6cos²αsin²α/ sin⁴α)+(sin⁴α/sin⁴α)}/{4(cos³αsinα/sin⁴α) – 4(cosαsin³α/sin⁴α)}

          cotan 4α = {cot⁴α – 6cot²α + 1}/{4cot³α – 4cotα}

61)         Sin 5α = sin5α + sinα - sinα
     = 2 sin3α cos2α - sinα
     = 2 (3sinα - 4sin³ α) (1 - 2sin² α) - sinα
     = 2 (8sin⁵ α - 10sin³ α + 3sinα) - sinα
Sin 5α = 16sin⁵ α - 20sin³ α + 5sinα (Terbukti)

62)         Sin 5α = sin(4α + α) = sin4α cosα + cos4α sinα
            = 2 sin2α cos2α cosα + (1 - 2sin² 2α) sinα
            = 4sinα cosα cos2α cosα + sinα - 2sin² α sinα
            = 4 sinα cos² α (1 - 2sin² α) + sinα - 2 (2sinα cosα)² sinα
            = 4 sinα (1 - sin² α) (1 - 2sin² α) + sinα - 2 (4sin² α cos² α) sinα
            = 4 sinα (1 - 3 sin² α + 2sin⁴ α) + sinα - 2 [4 sin³ α * (1 - sin² α)]
            = 4 sinα - 12sin³ α + 8sin⁵ α + sinα - 8sin³ α + 8 sin⁵ α
Sin 5α = 16 sin⁵ α - 20 sin³ α + 5 sinα. (Terbukti)

63)         Cos 5α = cos 5α + cosα - cosα
             = 2 cos3α cos2α - cosα
             = 2 (4cos³ α - 3cosα) (2cos² α - 1) - cos α
             = 2 (8cos⁵α - 10cos³ α + 3cos α) - cos α
Cos 5α = 16cos⁵ α - 20cos³ α + 5cosα (terbukti).

64)         Cos 5α = cos(2α +3α) = cos 2α.cos 3α – sin 2α.sin 3α = (2cos²α – 1) (4cos³α -3cosα) – 2sinα.cosα (3sinα – 4sin³α) = 8cos⁵α - 10cos³α + 3cosα – 6cosαsin²α +8cosαsin⁴α = 8cos⁵α - 10cos³α + 3cosα – 6cosα(1-cos²α) + 8cos(1-cos²α)²

        = 8cos⁵α - 10cos³α + 3cosα – 6cosα + 6cos³α + 8cos -16cos³α +8cos⁵α,

          Cos 5α = 16cos⁵ α - 20cos³ α + 5cosα

65)         Cos 5α = cos(2α +3α) = cos(2 α)cos(3 α) - sin(2 α)sin(3 α)
= (cos²α −sin²α) (cos³α −3sin²α cos α) − 2sin α cos α (3sin α cos² α −sin³ α)
= cos⁵α − 3sin² α cos³ α − sin² α cos³ α + 3sin⁴α cos α − 6sin² α cos³ α + 2sin⁴ α cos α
= 5sin⁴ α cos α − 10sin² α cos³ α + cos⁵α
= 5(1−cos² α)²cos α − 10(1−cos² α)cos³ α + cos⁵ α
= 5cos α (cos⁴ α −2cos² α +1) − 10cos³ α (1−cos² α) + cos⁵ α
= 5cos⁵ α − 10cos³ α + 5cos α − 10cos³ α + 10cos⁵ α + cos⁵ α

Cos 5α = 16cos⁵α − 20cos³ α + 5cos α (terbukti)

66)         Tan 5α = sin 5α/cos 5α
                  = (5 sin α - 20 sin³ α + 16 sin⁵ α)/(16cos⁵ α - 20cos³ α + 5cosα)
Tan 5α = (5tan α - 10 tan³α + tan⁵α)/ (1-10tan²α + 5tan⁴α) (Terbukti)

67)         Sin (6α) = sin (2 · 3α) = 2sin (3α) cos (3α)
sin (3α) = sin (2α + α) = sin (2α) cos (α) + cos (2α) sin (α)
cos (3α) = cos (2α + α) = cos (2α) cos (α) - sin (2α) cos (α)
sin (2α) = 2sin (α) cos (α)
cos (2α) = cos² (α) - sin² (α)
jadi, kita mendapatkan
2sin (3α) cos (3α) = 2 (sin (2α) cos (α) + cos (2α) sin (α)) (cos (2α) cos (α) - sin (2α) cos (α))
             = 2 (2sin (α) cos² (α) + cos² (α) sin (α) - sin³ (α)) (cos³ (α) -sin(α) cos²(α) - 2sin (α) cos²(α))
             = 2 (3sin (α) cos²(α) - sin³ (α)) (cos³ (α) - 3sin (α) cos²(α))
            = 2 [3sin (α) cos⁵ (α) -9sin² (α) cos⁵ (α) -3sin⁴ (α) cos² (α) + 3sin⁴ (α) cos (α)]
Sin 6α = 6sin (α) cos (α) [cos⁴ (α) - 3sin (α) cos⁴ (α) - sin³ (α) cos (α) + sin³ (α)] (terbukti)

68)         Sin(6α) = sin(3α + 3α) = 2sin(3α)cos(3α)
sin(3α) = sin(2α + α) = sin(2α)cos(α) + cos(2α)sin(α)
cos(3α) = cos(2α + α) = cos(2α)cos(α) - sin(2α)sin(α)
sin(2α) = 2sin(α)cos(α)
cos(2α) = cos²(α) - sin²(α)
sehingga sin(3α) = 2sin(α)cos²(α) + sin(α)cos²(α) - sin³(α) = 3sin(α)cos²(α) - sin³(α).
dan cos(3α) = cos³(α) - cos(α)sin²(α) - 2cos(α)sin²(α) = cos³(α) - 3cos(α)sin²(α).
sin(6α) = 2(3sin(α)cos²(α) - sin³(α))(cos³(α) - 3cos(α)sin²(α))
            = 2(3sin(α)cos⁵(α) - 9(cos(α)sin(α))³ - (sin(α)cos(α))³ + 3cos(α)sin⁵(α))
Sin 6α= 6sin(α)cos⁵(α) - 20(cos(α)sin(α))³ + 6cos(α)sin⁵(α)

69)         Sin 6α = sin (4α +2α) = sin4αcos2α + cos4αsin2α = 2sin2α.cos2α.cos2α + (1 – 2 sin²2α)sin2α = 2sin2α (1 – sin²2α) + (1 – 2sin²2α)sin2α = 2 sin2α – 2 sin³2α + sin2α – 2sin³2α = 3sin2α – 4sin³2α

70)         Cos 6α = cos 3(2α)

          cos 3α = 4 cos³α - 3cos α
cos 6α = 4 [ (2 cos² (α) - 1)³ - 3 ( 2 cos²(α) -1 ) ]
             = 4 [ 2 cos² (α) - (1)³ - 3( 2 cos²(α) )² + 3 ( 2 cos² (α) ] - 6 cos² (α) + 3
             = 4 [ 8 cos⁶ (α) - 1 - 12 cos⁴ (α) + 6 cos² (α) ] - 6 cos² (α) + 3
             = 32 cos⁶ (α) - 4 - 48 cos⁴ (α) + 24 cos² (α) - 6 cos² (α) + 3
             = 32 cos⁶ (α) - 48 cos⁴ (α) + 18 cos² (α) - 1
Cos 6α = 32 cos⁶ (α) - 48 cos⁴ (α) + 18 cos² (α) - 1 (terbukti)

71)         Cos 6α = cos(4α+2α)
            = cos4α cos2α-sin4α sin2α
            = [2cos²2α-1][2cos²α-1]-[2sin2αcos2α][2sinαcosα]
            = [2(2cos²α-1)²-1][2cos²α-1]-[2*2sinαcosα(2cos²α-1)][2sinαcosα]
            = [2(4cos⁴α-4cos²α+1)-1][2cos²α-1]-[8sin²αcos²α(2cos²α-1)]
            = [8cos⁴α-8cos²α+1][2cos²α-1]-[8(1-cos²α)cos²α(2cos²α-1)]
            = [16cos⁶α-8cos⁴α-16cos⁴α+8cos²α+2cos²α-1]-[(8cos²α-8cos⁴α)(2cos²α-1)]
            = [16cos⁶α-24cos⁴α+10cos²α-1]-[16cos⁴α-8cos²α-16cos⁶α+8cos⁴α]
            = [16cos⁶α-24cos⁴α+10cos²α-1]-[24cos⁴α-8cos²α-16cos⁶α]
Cos 6α= 32cos⁶α - 48cos⁴α + 18cos²α-1 (terbukti)

72)         cos 6α = 2cos²α 3α - 1
           = 2(4cos³α - 3cosα)² - 1
           = 2(16 cos⁶α + 9cos²α - 24cos²α) - 1
Cos 6α= 32cos⁶α - 48cos⁴α + 18cos²α-1 (terbukti)

73)         Sin 8α = sin 2(4α) kita tahu bahwa sin 2α = 2sinα.cosα

          Sin 2(4α) = 2 sin 4α.cos 4α sehingga

          Sin 4α = sin 2(2α) = 2sin2α.cos2α maka

          Sin 8α = 2{2sin 2αcos 2α}cos 4α = 4 sin 2αcos 2αcos 4α

          Memasukkan sin 2α = 2sinαcosα ke dalam persamaan

          = 2 sin 4αcos4α = 2(2sin2α.cos2α)cos 4α = 4 sin 2αcos 2αcos 4α = 4(2sinα.cosα)cos 2αcos 4α

          Sin 8α = 8sinα.cosα.cos2α.cos4α

74)         Cos 8α = cos(4α+4α) = cos 4α.cos4α – sin 4α.sin4α = cos²4α – sin²4α

75)         Cos 8α = cos²4α - sin²4α = (1-sin²4α) – sin²4α = 1 – 2 sin²4α

76)         Cos 8α = cos²4α – sin²4α = cos²4α – (1 – cos²4α) = 2cos²4α – 1.

77)         buktikan identitas berikut :sec 2α = ( cot α + tan α ) / (cot α - tan α)!

          = [ (cos α / sin α )+( sin α / cos α ) ] / [(cos α / sin α)-(sin α /cos α) ]
= [cos²( α ) + sin²( α) ] / [ cos²( α ) - sin²( α) ]
= 1 / ( cos (2α))
= sec (2α) 

78)         Tan 2α= (2 tan α)/(1-tan²α)

79)         Tan 3α = (3tan α - tan³α)/(1 - 3tan²α)

80)         Tan 4ɑ = {4tanα – 4 tan³α}/{1-6tan²α + tan⁴α}

81)         Tan 5α = (5tan α - 10 tan³α + tan⁵α)/ (1-10tan²α + 5tan⁴α)

82)         Tan 6α = (6tanα - 20tan³α + 6tan⁵α)/ (1-15tan²α + 15tan⁴α - tan⁶α)

83)         Tan 7α = (7tanα - 35tan³α + 21tan⁵α- tan⁷α)/(1-21tan²α + 35tan⁴α - 7tan⁶α)

84)         Tan 8α = (8tanα - 56tan³α + 56tan⁵α - 8tan⁷α)/(1-28tan²α + 70tan⁴α - 28tan⁶α + tan⁸α)

85)         Tan 9α = (9tanα - 84tan³α + 126tan⁵α -36tan⁷α + tan⁹α)/(1- 36tan²α + 126tan⁴α - 84tan⁶α + 9tan⁸α)

86)         Tan 10α = {10tanα – 120tan³α +252tan⁵α – 120tan⁷α + 10 tan⁹α}/{1 -45tan²α + 210tan⁴α – 120tan⁶α +45tan⁸α – tan¹°α}

87)         Buktikan bahwa {1 – tan²α}/{1+tan²α} = cos 2α

                     Ruas kiri = {1 – tan²α}/{1+tan²α} = {1-(sin²α/cos²α)}/{1+(sin²α/cos²α)}

                     = {(cos²α/cos²α)-(sin²α/cos²α)}/{(cos²α/cos²α) + (sin²α/cos²α)}

                     = (cos²α – sin²α) / (cos²α + sin²α) = cos 2α/1 = cos 2α ruas kanan

88)         Buktikan bahwa sin 2α = (2cot α)/(1+cot²α)

          Ruas kanan = (2cot α)/(1+cot²α) = {2(cos α/sinα)}/{1+(cos²α/sin²α)}

          = (2sin α.cos α)/(sin²α+cos²α) = 2 sinα.cosα = sin 2α  

89)         Buktikan bahwa {1 – tan²α}/{1+tan²α} = cos 2α

                     Ruas kiri = {1 – tan²α}/{1+tan²α} = {1-(sin²α/cos²α)}/{1+(sin²α/cos²α)}

                     = {(cos²α/cos²α)-(sin²α/cos²α)}/{(cos²α/cos²α) + (sin²α/cos²α)}

                     = (cos²α – sin²α) / (cos²α + sin²α) = cos 2α/1 = cos 2α ruas kanan

90)         Buktikan bahwa sin 2α = (2cot α)/(1+cot²α)

                     Ruas kanan = (2cot α)/(1+cot²α) = {2(cos α/sinα)}/{1+(cos²α/sin²α)}

                     = (2sin α.cos α)/(sin²α+cos²α) = 2 sinα.cosα = 2 sin α

91)         Cos 2α = 2cos²α – 1

92)         Cos 3α = 4cos³α – 3 cosα

93)         Cos 4α = 8 cos⁴α – 8 cos²α + 1

94)         Cos 5α = 16cos⁵α – 20 cos³α + 5 cos α.

95)         Cos 6α = 32cos⁶α – 48 cos⁴α + 18 cos²α – 1.

96)         Cos 7α = 64cos⁷α – 112 cos⁵α + 56 cos³α – 7cosα

97)         Cos 8α = 128cos⁸α – 256 cos⁶α + 160 cos⁴α – 32cos²α + 1

98)         Cos 9α = 256cos⁹α – 576 cos⁷α + 432 cos⁵α – 120cos³α + 9cosα

99)         Cos 10α = 512cos¹ᵒα – 1280 cos⁸α + 1120cos⁶α – 400cos⁴α + 50 cos²α – 1

100)     Sin 2α = 2sin α cosα

101)     Sin 3α = 3sinα – 4sin³α

102)     Sin 4α = 2sin 2α (1-2sin²α) = 2 sin 2α – 4sin2α sin²α = 4sinα.cosα – 8sin³αcosα

103)     Sin 5α = 5sin α – 20 sin³α + 16sin⁵α

104)     Sin 6α = 3sin 2α – 4sin³2α = 6sinα.cosα-32sin³αcosα+32sin⁵αcosα

105)     Sin 7α = 7sin α – 56sin³α + 112sin⁵α – 64 sin⁷α.

106)     Sin 8α= 8sinαcosα-80sin³αcosα+192sin⁵αcosα-128sin⁷αcosα

107)     Sin 9α = 9sinα-120sin³α+432sin⁵α-576sin⁷α+256sin⁹α

108)     Sin 10α = 10sinαcosα-160sin³αcosα+672sin⁵αcosα-1024sin⁷αcosα+5125sin⁹αcosα

109)     sin(3α) = 3 sin(α) - 4 sin³(α),

110)     cos(3α) = 4 cos³(α) - 3 cos(α),

111)     tan(3α) = [3 tan(α)-tan³(α)]/[1-3 tan²(α)]

112)     sin(4α) = 4 sin(α)cos(α)[2 cos²(α)-1],

113)     cos(4α) = 8 cos⁴(α) - 8 cos²(α) + 1.

114)     sin(5α) = 5 sin(α) - 20 sin³(α) + 16 sin⁵(α),

115)     cos(5α) = 16 cos⁵(α) - 20 cos³(α) + 5 cos(α).

116)     sin(6α) = 2 sin(α)cos(α)[16 cos⁴(α) - 16 cos²(α) + 3],

117)     cos(6α) = 32 cos⁶(α) - 48 cos⁴(α) + 18 cos²(α) - 1.

sin(nx) = 2 sin([n-1]x)cos(x) - sin([n-2]x),

cos(nx) = 2 cos([n-1]x)cos(x) - cos([n-2]x),

tan(nx) = (tan[(n-1)x]+tan[x])/(1-tan[(n-1)x]tan[x]) karena tan nx = tan{(n-1)x+x} jadi tan nx = tan{(n-1)x+x}={tan(n-1)x+tanx}/{1-tan(n-1)x.tanx} jika tan (n-1)x = H/k maka tan nx = {(h/k)+tan x}/{1-(H/k)tanx} maka

tan (nx) = {H+tanx.k}/{k-Htan x}

lanjutan Sudut Ganda atau rangkap part 2 klik disini